log（対数関数）の微分を誰でも理解できるように丁寧に解説

2021 4/17

2021年4月17日

対数関数 log の微分は、指数関数と並んで、微分学において重要な分野です。そこで、当ページではlogの微分について、誰でも理解できるように丁寧に開設していきたいと思います。

具体的には、以下のことがわかるようになります。

対数関数(log)とは何かが簡潔にわかる。
log の微分公式がわかる。
log の微分公式の証明がわかる。

なお、より理解を深めるには、当ページと、『指数関数の微分を誰でも理解できるように解説』を併せてご覧いただくのが良いでしょう。なぜなら、対数関数と指数関数は対になっているからです。

それでは、早速見ていきましょう。

1. 対数関数とは
1. 1.1. 対数（log）とは
2. 1.2. 対数関数とは
2. log の微分公式
1. 2.1. 対数関数 $\log_ax$ の微分公式
2. 2.2. 自然対数関数 $\log_ex$ の微分公式
3. log の微分の証明
1. 3.1. $\log_{a}x$ の微分の証明
2. 3.2. $\log_{e}x$ の微分の証明
4. logの微分のまとめ

1. 対数関数とは

対数関数は、身近な例だけでも、以下のような現象を表す重要な関数です。

水素イオンの指数を示すpH
騒音の程度を示すフォーン
地震の強さを示すマグニチュード
星の明るさを示す光度

また、その性質上、掛け算を足し算に変えるという特徴があるので、急激な変化を和らげる関数としても使われます。

ここでは、この対数関数に関して、以下の２点を簡潔におさらいしておきたいと思います。

対数(log)
対数関数

それでは早速見ていきましょう。

1.1. 対数（log）とは

対数とは、一言でいうと、指数関数における指数のことです。指数関数は以下の通り、指数部分が変数になっている関数のことでした。

指数

そして対数とは、この中から指数部分だけを抜き出して、以下のように書きあらためたもののことを言います。

対数

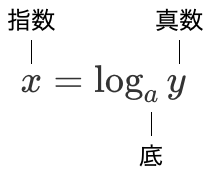
つまり対数とは、「 $y$ となるような $a$ の指数 $x$ は何か？」を示す値なのです。なお $\log$ 記号は、英語で対数を意味する “logarithm” の頭文字を取ったものです。以下で指数と対数を見比べてみましょう。

指数関数と対数関数の比較

$\begin{eqnarray} 2^1=2 \ \ &\longleftrightarrow& \ \ 1=\log_{2}2\\ 2^2=4 \ \ &\longleftrightarrow& \ \ 2=\log_{2}4\\ 2^3=8 \ \ &\longleftrightarrow& \ \ 3=\log_{2}8\\ &\vdots&\\ 2^x=y \ \ &\longleftrightarrow& \ \ x=\log_{2}y\\ \end{eqnarray}$

以上が対数 $\log$ です。

1.2. 対数関数とは

対数関数とは、底は一定で、真数の部分を変数 $x$ にしたもののことです。

対数関数

$f(x) = \log_{a}x\\ {}_{a>0, \ a\neq 1}$

この対数関数グラフは底が $a > 1$ の場合と、 $0 < a < 1$ の場合で異なります。

まず底が $a > 1$ の場合は下図のような曲線を描きます。ご覧のように、 $a$ の値が大きくなるほど、傾きが緩やかになっていきます。比較しやすくするために対となる指数関数も描いています。

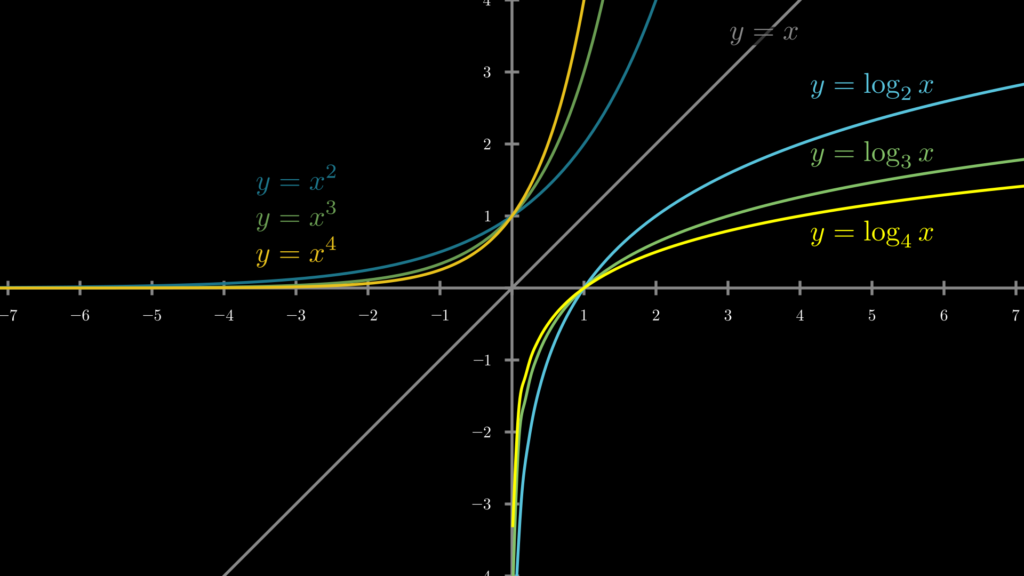
底が $0 < a < 1$ の場合はこれとは逆になります。

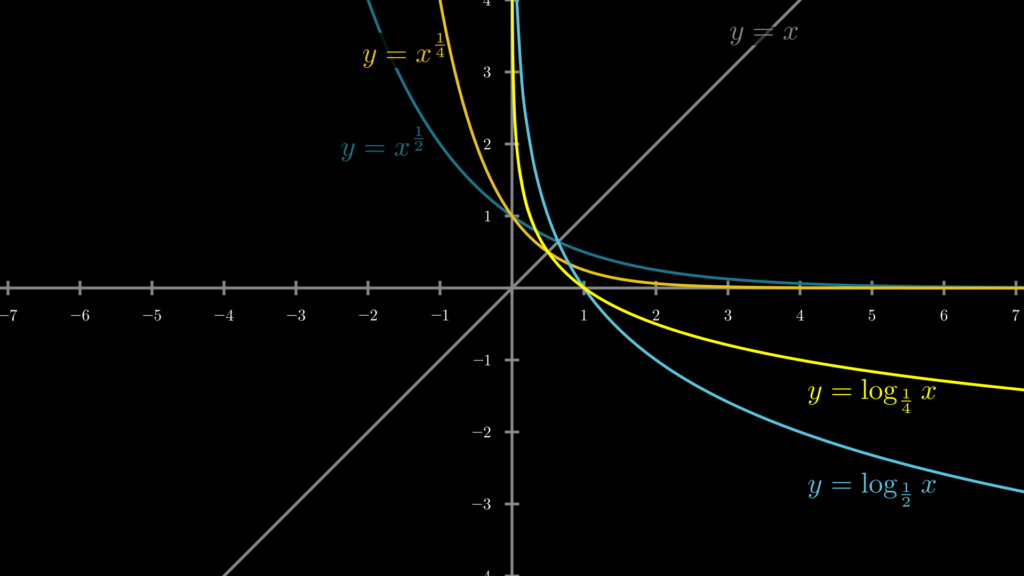
なお、 $\log x$ のように底の値が明示されていない場合は、底をネイピア数 $e$ とした自然対数 $\log_{e}a$ であることを意味します。ネイピア数 $e$ はとても面白い数字であり、次のような性質があります。

ネイピア数 $e$ と実数の関係

$\begin{eqnarray} n&=&e^{\log_{e}n}\\ &\vdots&\\ 2&=&e^{\log_{e}2}\\ 3&=&e^{\log_{e}3}\\ 4&=&e^{\log_{e}4}\\ \end{eqnarray}$

これについては、『指数関数の微分を誰でも理解できるように解説』でも詳しく触れているので、ぜひご確認ください。

2. log の微分公式

さて、それでは対数関数（log）の微分はどのようになるのでしょうか。ここでは、その微分公式と、実際の関数と導関数のグラフを確認しましょう。なお、公式は対数の底がネイピア数 $e$ の場合と、それ以外の場合で異なります（厳密には同じですが、底が $e$ の場合の方が楽になります）。

それでは見てみましょう。

2.1. 対数関数 $\log_ax$ の微分公式

対数関数の微分公式は次の通りです。

対数関数の微分公式

$(\log_a x)^{\prime}=\dfrac{1}{x \log_e a}$

底が $2$ の場合のグラフを確認してみましょう。

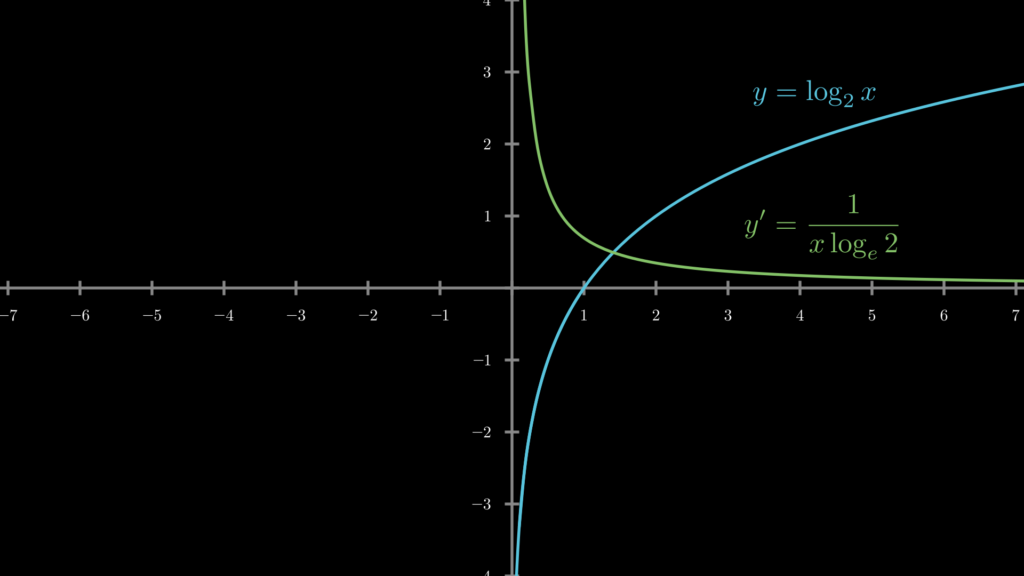
2.2. 自然対数関数 $\log_ex$ の微分公式

次に対数の底がネイピア数 $e$ の場合は、次の通りになります。

自然対数関数の微分公式

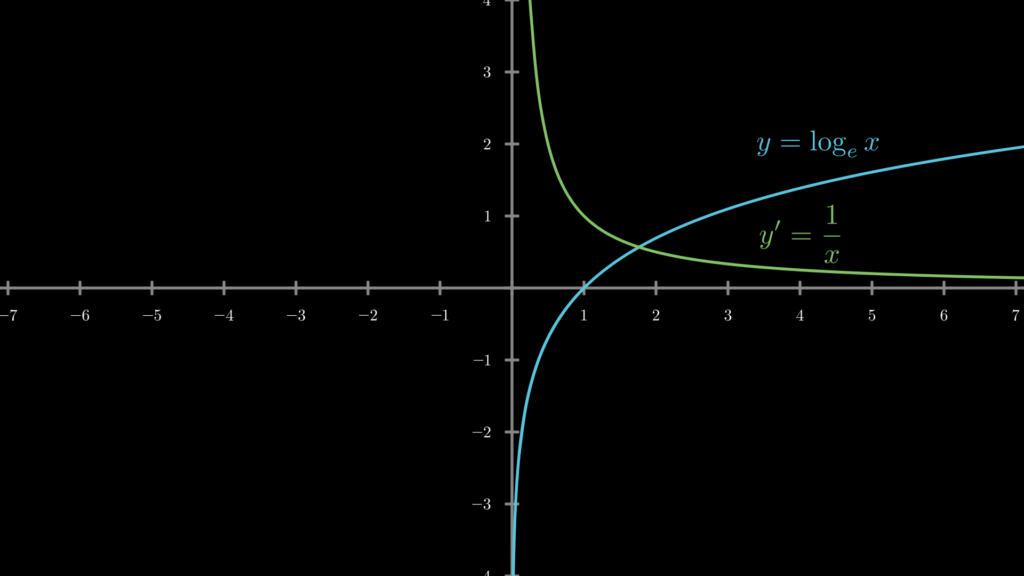
$(\log x)^{\prime}=\dfrac{1}{x}$

グラフで視覚的に確認してみましょう。

3. log の微分の証明

それでは、対数関数 log の微分は、なぜこれらの公式で求められるのでしょうか。ここでは、この点について考えていきましょう。

3.1. $\log_{a}x$ の微分の証明

底がネイピア数 $e$ ではない対数関数 $\log_{a}x$ の微分を、微分の定義式を使って求めてみましょう。すると、以下のようになります。

対数関数 $\log_{a}x$ の微分を定義式から求める①

$\begin{eqnarray} (\log_{a}x)^{\prime} &=& \dfrac{\log_{a}(x+dx)-\log_{a}(x)}{dx}\\ &=& \dfrac{1}{dx} \left \{ \log_{a}(x+dx)-\log_{a}(x) \right \}\\ &=& \dfrac{1}{dx} \log_{a}\left( \dfrac{x+dx}{x} \right)\\ &=& \dfrac{1}{dx} \log_{a}\left( 1+ \dfrac{dx}{x} \right)\\ &=& \log_{a}\left( 1+ \dfrac{dx}{x} \right)^{\frac{1}{dx}} \end{eqnarray}$

※ 3段目は対数公式 $\log_aM-\log_aN=log_a \frac{M}{N}$ より。
※ 5段目は対数公式： $k\log_aM=\log_aM^k$ より。

ここで、 $\frac{dx}{x}=dX$ と置きます。 $dx$ はほぼ $0$ である値なので、 $dX$ もほぼ $0$ になります。そのため、次のように数式を変換することが可能です。

対数関数 $\log_{a}x$ の微分を定義式から求める②

$\begin{eqnarray} \log_{a}\left( 1+ \dfrac{dx}{x} \right)^{\frac{1}{dx}} &=& \log_{a}(1+dX)^{\frac{1}{x \cdot dX}}\\ &=& \log_{a} \{(1+dX)^{\frac{1}{dX}} \}^{\frac{1}{x}} \end{eqnarray}$

※ 1段目の指数部分は $\frac{dx}{x}=dX$ より $dx=x \cdot dX$ となる。
※ 2段目は指数公式 $a^{mn}=(a^m)^n$ より。

さて、ここで $\log$ に渡している値 $(1+dX)^{\frac{1}{dX}}$ に注目してみましょう。そう、これはネイピア数 $e$ の定義そのものになっています（これを計算すると $2.718 \cdots$ という数字が現れます）。

このことから以下のように変換することができます。

対数関数 $\log_{a}x$ の微分を定義式から求める③

$\begin{eqnarray} \log_{a} \{(1+dX)^{\frac{1}{dX}} \}^{\frac{1}{x}} &=& \log_{a} e^{\frac{1}{x}} \\ &=& \dfrac{1}{x} \log_{a}e\\ &=& \dfrac{1}{x} \dfrac{1}{\log_{e}a}\\ &=& \dfrac{1}{x\log_{e}a} \end{eqnarray}$