ベクトルの掛け算とは簡単に言うと、「ベクトルの向きはそのままで、長さを伸ばしたり縮めたりすること」です。
これはベクトルの和と並んで、線形代数において基礎となる重要な計算です。なぜなら、あらゆるものごとを線形代数的に分析するための土台（「線形空間」と言います）が、このベクトルの和とベクトルの掛け算から成り立っているからです。
そこで、このページでは、これらについてアニメーションを用いながら、ベクトルの掛け算について、視覚的にもわかりやすく解説していきます。ぜひお役立ていただければと思います。
なお、ベクトルの和については『ベクトルの和とは何か？誰でもわかる幾何学的な意味と計算方法の解説』で解説しているので、ぜひ一緒に確認しておきましょう。
1. ベクトルの掛け算とは
まずはベクトルの掛け算とはどういうものなのかを、幾何学的にイメージできるようにしましょう。繰り返しになりますが、これは「ベクトルの向きはそのままで、長さを伸ばしたり縮めたりすること」と同じです。
このことは以下のアニメーションを見て頂くとすぐに理解することができます。
以下に、\(\vec{v}\)、 \(2\cdot\vec{v}\)、\(-2\cdot\vec{v}\) の画像も載せておきます。
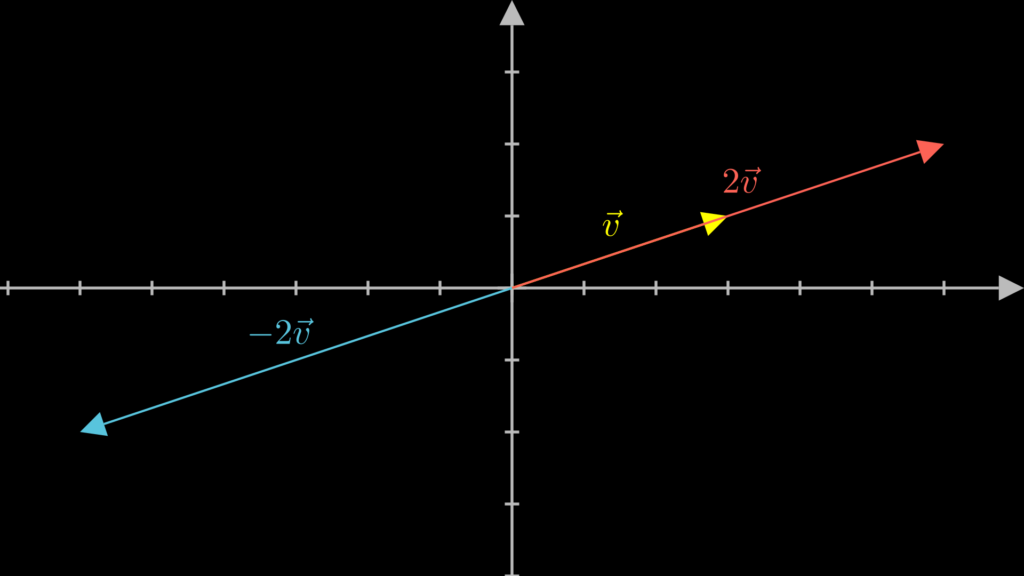
三次元ベクトルでも同じです。
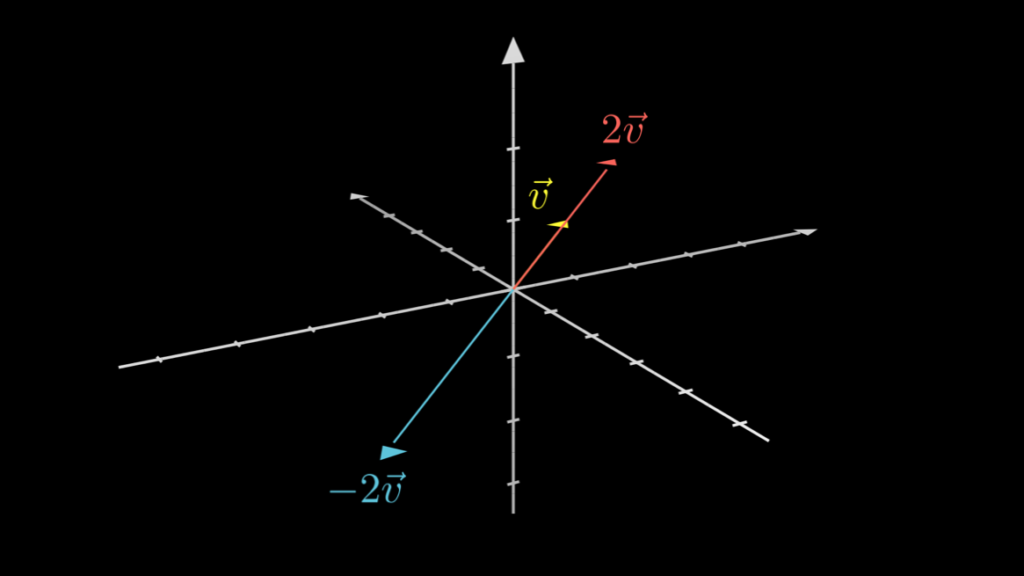
このようにベクトルの掛け算とは「ベクトルの向きはそのままで、長さを伸ばしたり縮めたりすること」なのです。
【補足】スケーリング・スカラー・スカラー倍
ここまで見てきたように、ベクトルの掛け算によってベクトルの長さを伸ばしたり縮めたりすることを「スケーリング」と言います。そして、線形代数においては数値の主な目的はスケーリングなので、「数値」ではなく「スカラー」と呼ぶことが慣例になっています。そのため、ベクトルの掛け算のことを「スカラー倍」と言います。
2. ベクトルの掛け算の計算方法
それでは、次にベクトルの掛け算を数値で理解していきましょう。これも結論から言うと、ベクトルの掛け算は次のように成分ごとにスカラー倍することで計算します。
２次元ベクトルの掛け算と３次元ベクトルの掛け算
\[\begin{eqnarray}
s\left[ \begin{array}{c} v_1 \\ v_2 \end{array} \right]
=
\left[ \begin{array}{c} sv_1 \\ sv_2 \end{array} \right],
\hspace{3mm}
s\left[ \begin{array}{c} v_1 \\ v_2 \\ v_3 \end{array} \right]
=
\left[ \begin{array}{c} sv_1 \\ sv_2 \\ sv_3 \end{array} \right]
\end{eqnarray}\]
この計算方法については、以下のアニメーションをご覧頂くと理解を深めることができます。
参考のためにベクトルの掛け算を行っているシーンの画像を以下に載せておきます。
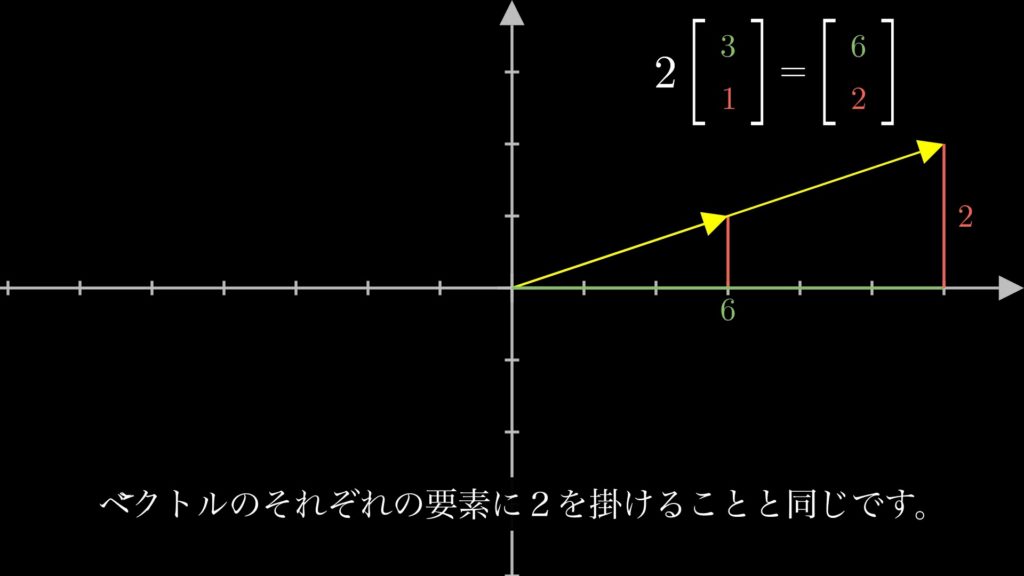
三次元ベクトルでもそれ以上のベクトルでも、成分ごとにスカラー倍するという点はもちろん変わりません。以下の画像でご確認ください。
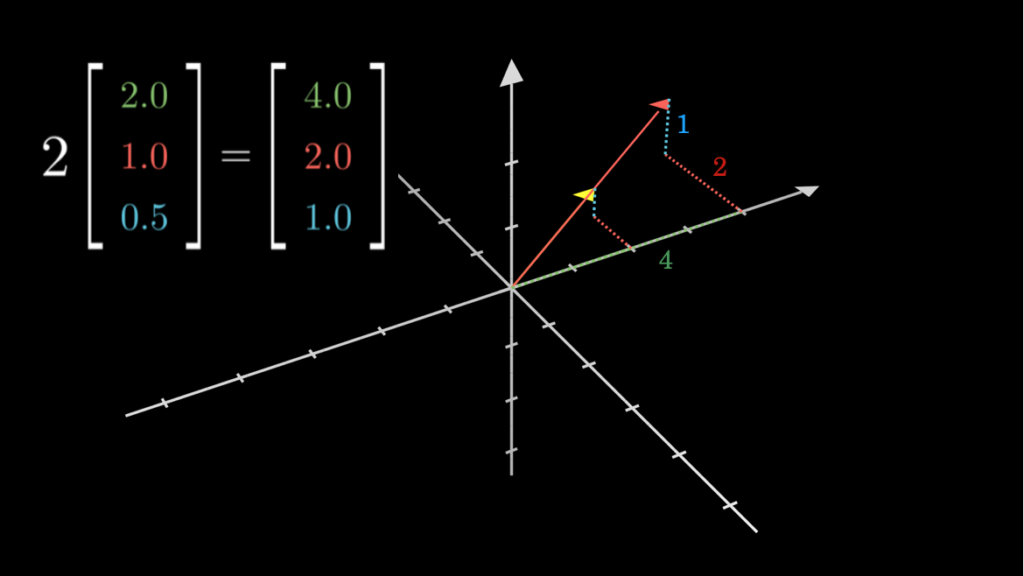
以上がベクトルの掛け算の計算方法です。
3. ベクトルの掛け算の性質
なお、ベクトルの掛け算には、いくつか知っておきたい性質があります。それが以下です。
- \(1\vec{v}=\vec{v}\)
- \((s_1s_2)\vec{v}=s_1(s_2\vec{v})\)
- \(s(\vec{v}+\vec{w})=s\vec{v}+s\vec{w}\)
- \((s_1+s_2)\vec{v}=s_1\vec{v}+s_2\vec{v}\)
これらの性質は、アニメーションで視覚的に確認すると簡単に理解することができます。それぞれ見ていきましょう。
なお、\(1\vec{v}=\vec{v}\) については、アニメーションがなくとも、当たり前のこととして理解できると思いますので省くことにします。
\((s_1s_2)\vec{v}=s_1(s_2\vec{v})\)
計算例
\[\begin{eqnarray}
(2\times1.5)\left[ \begin{array}{c} 2 \\ 1 \end{array} \right]
&=&
3\left[ \begin{array}{c} 2 \\ 1 \end{array} \right]
=
\left[ \begin{array}{c} 6 \\ 3 \end{array} \right] \\
&\upharpoonleft\downharpoonright& \\
2(1.5\left[ \begin{array}{c} 2 \\ 1 \end{array} \right])
&=&
2(\left[ \begin{array}{c} 3 \\ 1.5 \end{array} \right])
=
\left[ \begin{array}{c} 6 \\ 3 \end{array} \right]
\end{eqnarray}\]
\(s(\vec{v}+\vec{w})=s\vec{v}+s\vec{w}\)
計算例
\[\begin{eqnarray}
2\left(
\left[ \begin{array}{c} 2 \\ 1 \end{array} \right]
+
\left[ \begin{array}{c} 1 \\ -2 \end{array} \right]
\right)
&=&
2\left[ \begin{array}{c} 3 \\ -1 \end{array} \right]
=
\left[ \begin{array}{c} 6 \\ -2 \end{array} \right]\\
&\upharpoonleft\downharpoonright& \\
2\left[ \begin{array}{c} 2 \\ 1 \end{array} \right]
+
2\left[ \begin{array}{c} 1 \\ -2 \end{array} \right]
&=&
\left[ \begin{array}{c} 4\\ 2 \end{array} \right]
+
\left[ \begin{array}{c} 2 \\ -4 \end{array} \right]
=
\left[ \begin{array}{c} 6 \\ -2 \end{array} \right]
\end{eqnarray}\]
\((s_1+s_2)\vec{v}=s_1\vec{v}+s_2\vec{v}\)
計算例
\[\begin{eqnarray}
(-3+5)
\left[ \begin{array}{c} 1 \\ 0.6 \end{array} \right]
&=&
2\left[ \begin{array}{c} 1 \\ 0.6 \end{array} \right]
=
\left[ \begin{array}{c} 2 \\ 1.2 \end{array} \right]\\
&\upharpoonleft\downharpoonright& \\
-3\left[ \begin{array}{c} 1 \\ 0.6 \end{array} \right]
+
5\left[ \begin{array}{c} 1 \\ 0.6 \end{array} \right]
&=&
\left[ \begin{array}{c} -3\\ -1.8 \end{array} \right]
+
\left[ \begin{array}{c} 5 \\ 3 \end{array} \right]
=
\left[ \begin{array}{c} 2 \\ 1.2 \end{array} \right]
\end{eqnarray}\]
4. ベクトルの掛け算の練習問題
最後に練習問題を用意しておきますので、理解を深めるために一度ご自身で解いてみてください。以下のボックスをクリックすると、問題と解答を確認することができます。
5. まとめ
以上がベクトルの掛け算（スカラー倍）です。
アニメーションでご覧いただいたように、まずは、これを幾何学的にイメージできるようになっていることが大事です。その上で、計算方法もしっかりと抑えておきましょう。
次に読みたいページ
次の記事として『ベクトルの分解とは？その方法と幾何学的な意味の解説』をご覧ください。これまで学んだベクトルの和や掛け算の知識がさっそく活きることになります。
：Pythonの基本をおさえた人が、実際に機械学習やディープラーニングを活用できるようになるための講座。転職補償型があるなどキャリア支援の内容が非常に手厚く、講師の質も最高クラス。コスパ最高。Python初心者用の対策講座もある。
コメント