ベクトルの座標とは、あるベクトルの長さと向きを数字の組み合わせで表すための概念です。
少しおさらいですが、前回の記事『ベクトルとは一体なに?その意味と定義が深く理解できる解説』で解説したように、ベクトルとは長さと向きをもつ矢印です。しかし、ベクトルを常に矢印で表すのは不都合です。なぜなら、そのままではベクトルの和や掛け算などの計算を行うことができないからです。
この問題を解決するのが「座標系」であり、「ベクトルの座標」です。当ページでは、これについて、アニメーションを使いながら、視覚的にもわかりやすく解説します。
1. 座標系とは
線形代数では、ベクトルは「座標系」に存在するものとして扱います。それでは座標系とは何でしょうか?
座標系とは、たとえば二次元空間の場合は、水平軸(\(x\)軸)と垂直軸(\(y\)軸)の二つの成分が存在する平面空間のことです。三次元空間の場合は、これに高さ軸(\(z\)軸)が加わった三つの成分が存在する立体空間のことです。
以下のアニメーションを見て頂くと、すぐに理解できるでしょう。
これが座標系です。
この座標系があって初めて、ベクトルの長さと向きを「座標」という指標で表すことが可能になります。次からこの点について見ていきましょう。
2. ベクトルの座標とは
ベクトルを座標系の中に存在するものであると考えると、ベクトルの長さと向きを座標で表すことができるようになります。これについては以下のアニメーションで視覚的に解説しています。
視覚的に確認することで、具体的に理解できるようになりますので、ぜひご覧ください。
念のため文字でも解説しておきます。
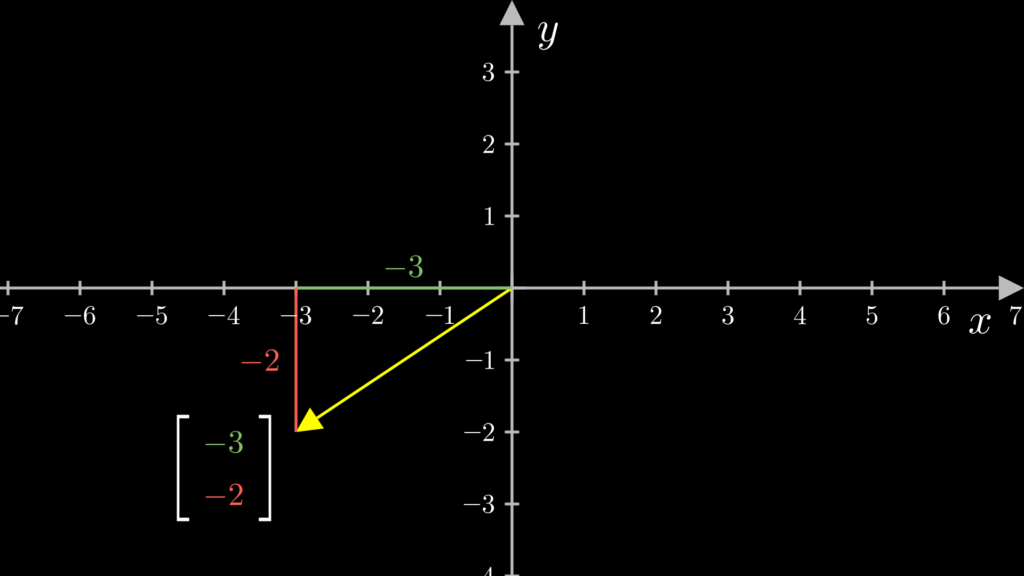
例えば2次元ベクトルの場合は、原点からベクトルの先端までの長さを、そのベクトルの水平成分の長さ(\(x\)軸方向の長さ)と、垂直成分の長さ(\(y\)軸方向の長さ)の2つの成分で表現します。そして以下のように、それらの成分を縦に並べ、括弧で囲ったものがベクトルの座標です。
\[
\left[ \begin{array}{cc} x \\ y \end{array} \right]
\]
例えば、水平成分が \(-3\)、垂直成分が \(-2\) のベクトルの座標は \(\left[ \begin{array}{cc} -3 \\ -2 \end{array} \right]\) になります。
3次元ベクトルは、これに高さ成分の長さ(\(z\)軸方向の長さ)を加えて、以下のように表します。
\[
\left[ \begin{array}{cc} x \\ y \\ z\end{array} \right]
\]
以下の画像でご確認ください。
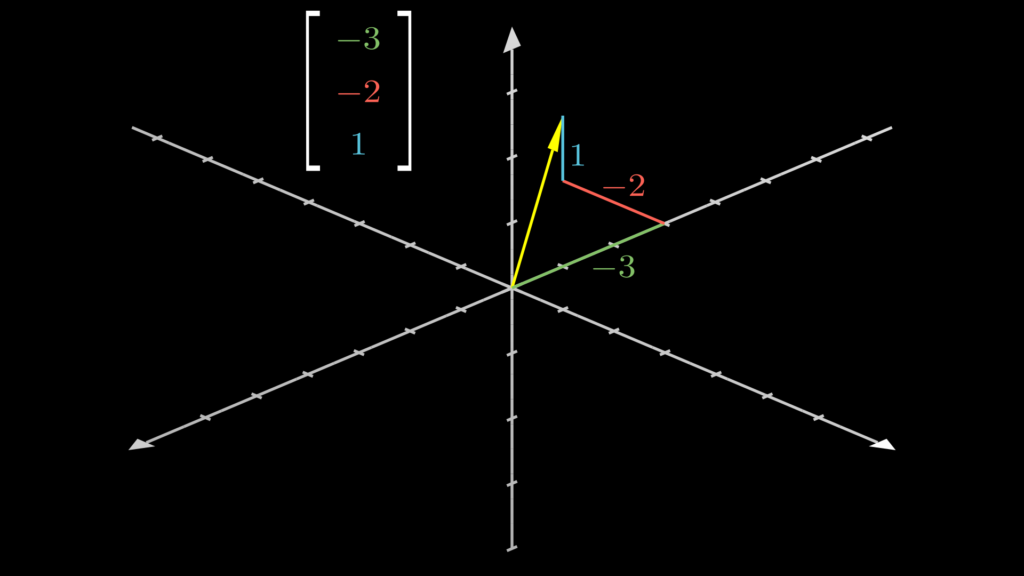
なお、大事な原則として、ある一つのベクトルは一つの座標でのみ示すことができます。そして、一つの座標は一つのベクトルのみを示します。言われてみると当たり前のことですが覚えておきましょう。
3. まとめ
以上のようにベクトルの座標とは、ベクトルの長さと向きを数値の並びで示したものです。この座標を使うことではじめて、線形代数において非常に重要な計算であるベクトルの和とベクトルの積を行うことが可能になります。
次に読みたいページ
このようにベクトルと座標を理解することで、ベクトルの計算が可能になります。特に線形代数においては、ベクトルの和と積の計算は必要不可欠な概念です。そこで次は『ベクトルの和とは何か?誰でもわかる幾何学的な意味と計算方法の解説』でベクトルの和とは何かとその計算方法について学びましょう。








コメント